Power Law

당신은 서로 아는 사람이 한 명도 없는 백 명의 손님을 초대해 성대한 파티를 열었습니다. 디너 파티에 적합한 음식과 치즈, 페어링되는 와인을 마련하면, 그들은 만나서 서로 알고자 하는 본능에 따라 2-3명씩 모여 오손도손 이야기를 시작할 것입니다. 이제 지나가는 한 손님에게 당신의 비밀을 하나 알려줍니다. 라벨이 붙지 않은 진홍색의 병에는 최고급 와인이 들어있고, 다른 병의 와인보다 훨씬 좋다는 것입니다. 그리고 이 정보를 새로 사귄 손님들에게만 공유하도록 요구합니다.
당신은 비밀이 퍼지는데는 시간이 오래 걸리고 고급 와인이 안전하리라 생각할 수 있습니다. 한 사람씩 이야기를 나누며 10분마다 다른 그룹으로 떠나도 모든 사람을 만나려면 16시간 반은 걸릴테니 말이죠. 하지만 이내 생면부지의 사람들 간에 미묘한 네트워크의 경로가 형성되기 시작하고, 한 시간이 채 되지 않아 백 명의 모든 손님을 포괄하는 그물망이 형성됩니다. 당신의 비밀이 공공연한 소문이 되는데는 30분도 필요하지 않고, 고급 와인은 금새 동이 날 것입니다.
여기서 각 손님은 노드이고 새로운 만남이 이뤄질 때마다 그들간에 사회적 연결선link이 생겨나며 하나의 그래프가 형성됩니다. 재밌는 점은 링크를 하나씩 더해가다 보면 어느새 여러 노드가 얽힌 클러스터가 생겨난다는 사실입니다. 만약 노드의 개수 만큼의 링크가 추가된다면 보통 하나의 거대한 클러스터가 등장하는데, 이는 비밀이 순식간에 소문이 되는 강력한 네트워크입니다. 이러한 현상은 인간의 사회망 뿐만 아니라, 전선으로 연결된 컴퓨터들, 축삭돌기로 연결된 뉴런들과 같은 복잡계에서도 흔히 나타나는데, 그 기저엔 Power Law라고 불리우는 세상의 중요한 원리가 숨어 있습니다.
World of Standard Normal Distribution
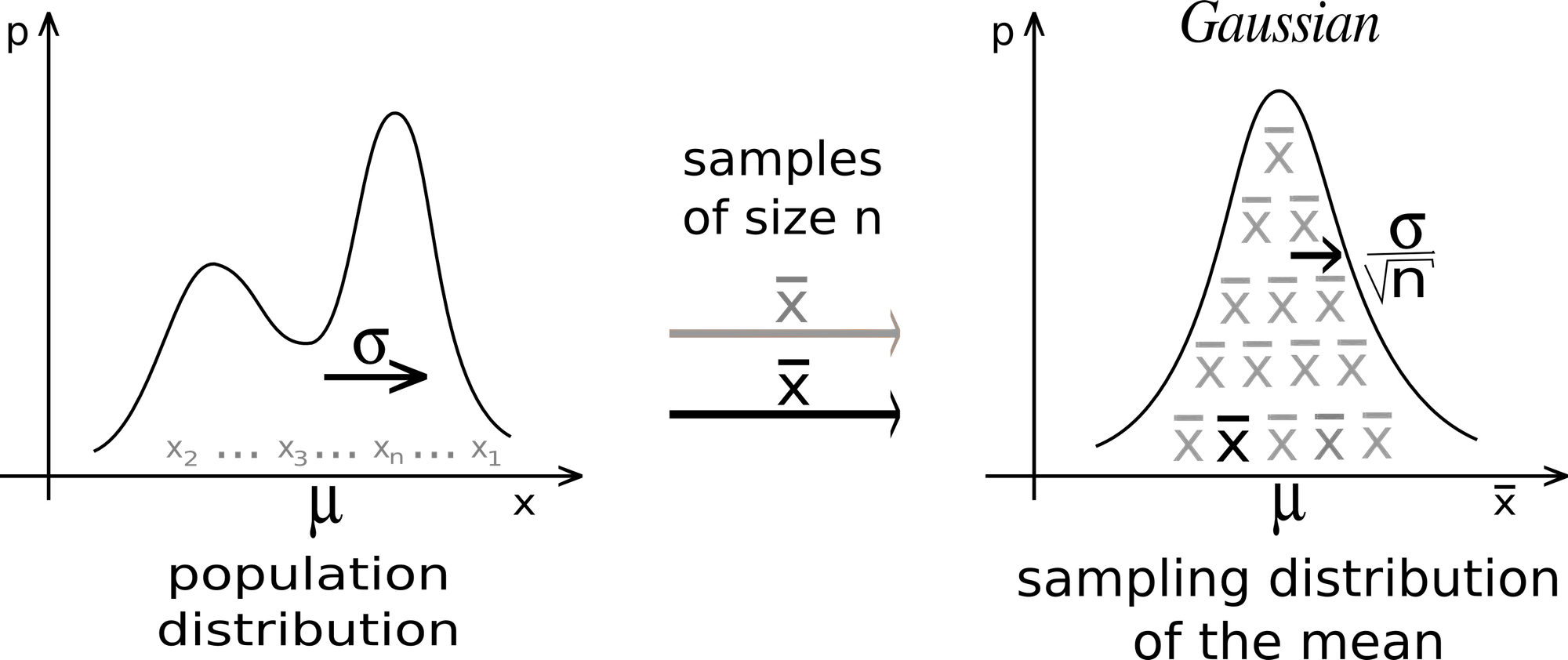
우리는 세상을 설명하는 핵심적인 모델로 정규 분포Normal Distribution를 알고 있습니다. 학창시절에 배우는 중심 극한 정리Central Limit Theorem은 ‘동일한 확률분포를 가진 독립 확률변수 n개의 평균의 분포는 n이 적당히 크다면 정규분포에 가까워진다’는 내용을 담고 있는데, 이는 상당히 일반적으로 적용이 가능한 정리여서 세상을 잘 설명해주는 진리에 가까워 보이기도 합니다.
예를 들어, 성인 남성의 키를 측정해 각 키 구간별 빈도의 분포를 구해보면 97%가 넘는 사람은 160-185cm에 분포해 있고, 특별히 농구 선수만 표본을 추출하지만 않는 한 200cm를 넘는 사람은 극히 드물 것입니다. IQ에서 기체의 분자 속도에 이르기까지 자연의 많은 분포는 이러한 정규 분포를 따릅니다. 이는 종형 분포Bell Curve가 ‘정규Normal’ 분포로 불리우는 이유이기도 합니다.
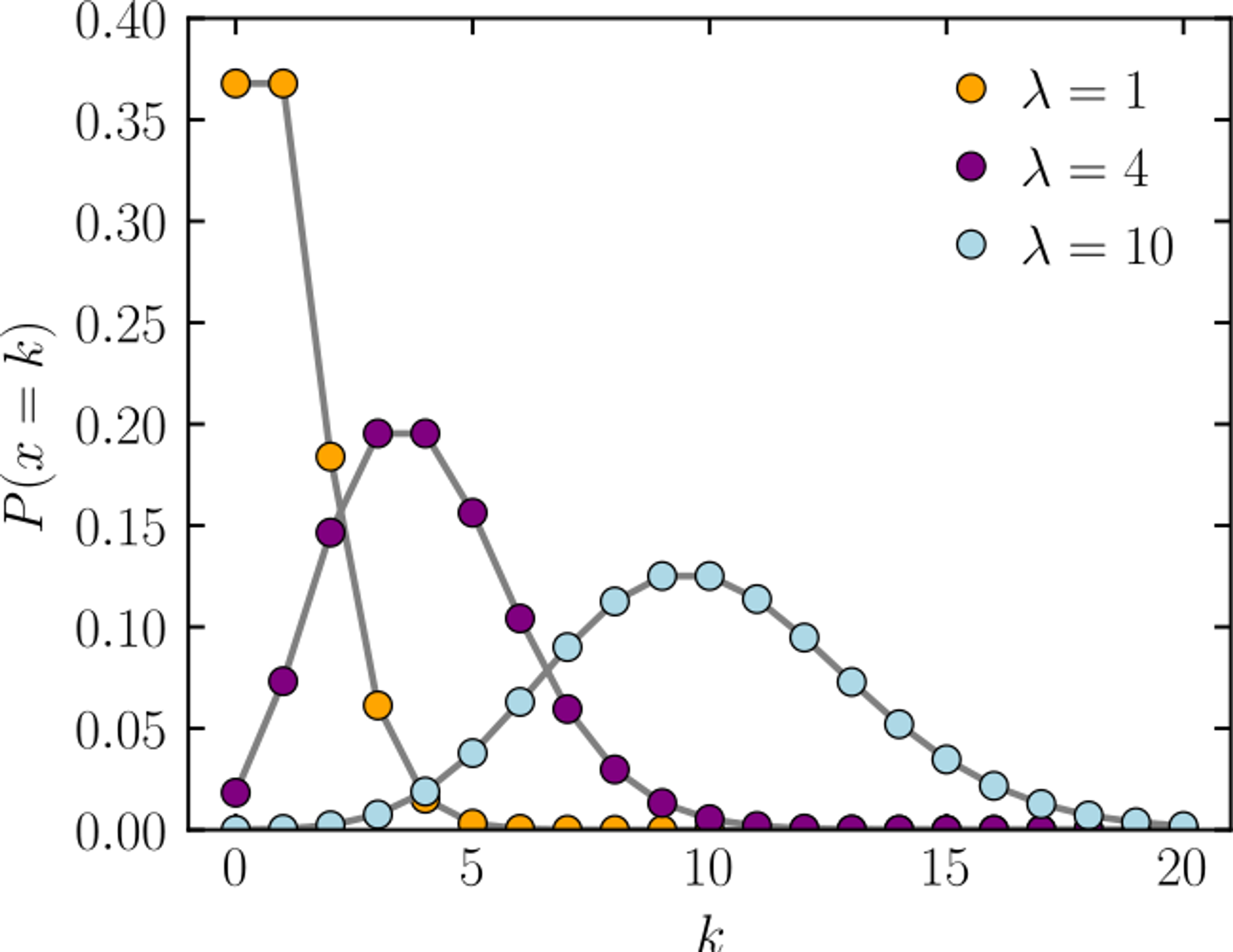
같은 결에서, 이산적인 값을 다루는 푸아송 분포Poisson Distribution도 있습니다. 이 역시 눈에 띄는 정점을 중심으로 평균에 몰린 분포를 모델링하는데 자주 사용됩니다. 이 정점의 양쪽 사면에서는 분포가 지수함수적으로 감소하는데, 이는 정규분포와 마찬가지로 평균에서 상당히 멀리 떨어지는 경우가 극히 드물다는 것을 의미합니다.
무작위적 그래프 이론과 그 네트워크 모델은 철저히 평등주의적입니다. 주사위 던지기를 통해 노드와 노드를 잇는 엣지, 혹은 링크는 무작위적으로 부여됩니다. 즉, 우리 모두는 라스베이거스의 카지노에서 잭팟을 터트리고, 다음 회차 연금 복권에서 우승할 기회를 똑같이 부여받은 것입니다. 물론 하루의 막이 내리면 그 중 소수만이 잭팟을 터트린 부자가 됩니다. 하지만 여전히, 거의 모든 노드는 같은 수의 링크를 가지게 될 것입니다.
다시 말해, 정규 분포나 푸아송 분포로 설명되는 무작위적 세계는 평균에 의해 지배되는 세계입니다. <링크>에 따르면, 이는 대부분의 사람은 거의 같은 수의 아는 사람을 가지며, 대부분의 뉴런은 거의 같은 수의 다른 뉴런과 연결되어 있고, 대부분의 기업은 거의 같은 수의 다른 기업과 거래관계를 맺으며, 대부분의 웹사이트는 거의 같은 수의 방문객을 갖게 된다고 예측하는 것입니다.
하지만 알베르트 아인슈타인은 “신은 이 세계를 가지고 주사위 놀이를 하지 않는다.”고 말했습니다. 플라톤주의자로서, 저 역시 같은 믿음을 가지고 다른 모델에 주목해보려 합니다. 우리는 이미 이러한 종형 곡선Bell Curve이 설명하지 못하는 세상의 중요한 시스템, 혹은 계를 많이 알고 있습니다. 그리고 그 중심에는 ax^(-k) 무리함수 꼴의 Power-law Distribution거듭제곱 법칙 분포가 놓여 있습니다. Power Law, 혹은 거듭제곱 법칙은 부자는 더 부유해지고 가난한 사람은 더 빈곤해지는 양성 피드백의 세계를 설명합니다.
오류가 발생하는 지점은 벤처기업의 수익이 정규분포를 따를 거라고 기대하는 데 있다. 다시 말해 형편없는 회사는 실패하고, 보통인 회사는 평범한 수익을 내고, 훌륭한 회사는 2배 혹은 4배까지의 수익을 낼 거라고 예상하는 것이다. 이렇게 단조로운 패턴을 생각하는 투자자들은 다각화된 포트폴리오를 구성한 다음, 성공작의 수익이 실패작의 손실을 상쇄해주기를 바란다.
그러나 이렇게 ‘분산시켜놓고 기도하는’ 식의 접근법은 보통 실패작만 가득 모아놓은 포트폴리오를 구성하게 되기 십상이다. 히트작은 하나도 없는 것이다. 이렇게 되는 이유는 벤처기업의 수익이 전체적으로 정규분포를 따르지 않기 때문이다.
<제로 투 원Zero to One>, 피터 틸Peter Thiel
Pareto Principle, or 80/20 Rule
1900년대 초 제네바에서 열린 한 경제 회의에서 이탈리아의 영향력 있는 경제학자 빌프레도 파레토Vilfredo Pareto가 자신의 논문을 발표하고 있었다.
…
파레토는 20년 동안 철도 엔지니어로 일한 후 경제학으로 관심을 전환했다. 뉴턴 물리학의 수학적 아름다움으로부터 깊은 감명을 받은 그는 경제학을 아이작 뉴턴의 <프린키피아Principia>에서 정식화되어 있는 것과 같은 보편적인 법칙들로 서술될 수 있는 엄밀한 과학으로 전환시키겠다는 꿈을 위해 그의 여생을 바쳤다.
그의 지칠줄 모르는 탐구의 결실인 세 권짜리 <트라타토Trattato>는 경제학자들과 사회학자들 모두에게 끝없는 영감과 해석의 원천이 되고 있다.
<링크Linked>, A.L. 바라바시Barabási
이탈리아의 경제학자 빌프레도 파레토는 그의 경험적 관찰들에 대한 기술이 후대에 “파레토 법칙Pareto Principle”으로 재해석되며 대중들에게 널리 알려졌습니다. 1906년에 파레토는 20%의 사람들이 이탈리아 땅의 80%를 소유하고 있음을 알아챘는데, 이는 원예사로서 그의 정원에 있는 단 20%의 콩깍지가 80%의 완두콩을 생산하는 것과 유추를 이루었습니다.
이러한 파레토 법칙은 80/20 Rule로도 알려져 있습니다. 이는 CS의 80%는 고객의 20%에게서 나오며, 기업의 수익 중 80%는 20%의 고객에게서 창출된다, 또한 범죄의 80%는 범죄자 중 20%에 의해 저질러지고 웹 링크의 80%는 15%의 웹페이지를 향한다는 등 다양한 영역에 적용되며 그 간단하지만 강력한 표현을 통해 널리 알려졌습니다.
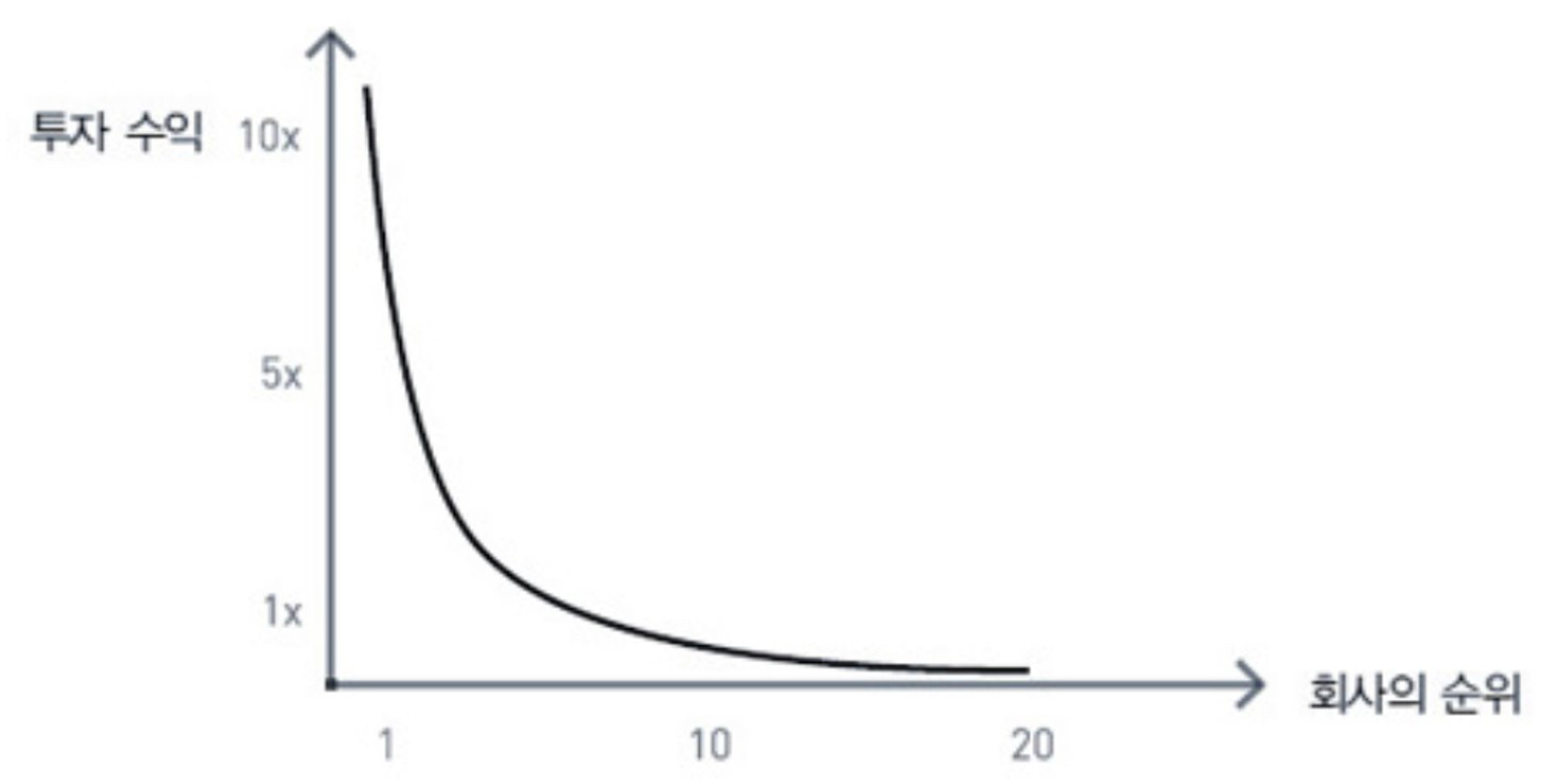
”벤처캐피털계의 가장 큰 비밀은, 성공한 펀드는 가장 잘한 투자가 나머지 모두를 합친 것과 같거나 그보다도 더 큰 수익을 낸다는 점이다.”
…
얼마 안 되는 소수가 다른 경쟁자들을 압도적으로 능가하는 이 엄연한 패턴은 자연 상태와 사회 상태를 가릴 것 없이 우리 주변 어디에서나 볼 수 있다. 예를 들면 가장 파괴적인 지진은 작은 지진들을 모두 합친 것보다 몇 배나 더 강력한 힘을 발휘한다. 대도시들은 작은 마을을 모두 모아놓은 것보다도 훨씬 크다. 그리고 독점기업은 무차별한 수백만의 경쟁자들보다 더 많은 가치를 차지한다.
아인슈타인이 뭐라고 했건, 혹은 안 했건 거듭제곱 법칙power law은 우주의 법칙이다. 우리 주변은 전적으로 이 법칙에 따라 만들어져 있기 때문에 우리는 미처 그렇다는 사실조차 눈치채지 못하고 있다.
<제로 투 원Zero to One>, 피터 틸Peter Thiel
현실 세계에서 파레토 법칙을 따르는 시스템은 다소 특별하고, 복잡한 네트워크를 이해하는 핵심과 맞닿아 있기에 주목할 만한 가치가 있습니다. 파레토 법칙은 거듭제곱 법칙 분포의 특수한 한 형태로서 그 핵심을 잘 드러내고 있습니다.
베이조스가 엄청난 재산을 모으면 더욱 부유해질 기회가 몇 배나 많아진다. 과학논문이 많이 인용될수록 더욱 알려져서 훨씬 더 많이 인용된다. 성공할 기회가 몇 배나 더 많아지는 아웃라이어라면, 정규분포의 영역을 멱법칙이 지배하는 영역, 즉 사물이 조금 변하는 세상에서 크게 변하는 세상으로 전환시킬 수 있다.
…
이 기간에 전체 자본투자의 5퍼센트밖에 안 되는 투자에서 이 회사가 벌어들인 총수익의 60퍼센트를 벌어들였다. … Y Combinator의 경우에는 2012년에 280건의 투자 중 불과 2퍼센트에서 총수익의 4분의 3이 발생했다.
…
인구의 10퍼센트만이 부의 80퍼센트 혹은 90퍼센트를 보유할 수도 있다. 그러나 정확한 숫자가 무엇이 되었든 이 모든 분포가 멱법칙power law의 사례들이다. 승자가 선형이 아니라 기하급수적으로 빠르게 발전하기 때문에 이렇게 불리는 것이다.
<The Power Law: Venture Capital and the Making of the New Future>, Sebastian Mallaby
Power law
y = ax^(-k) + b 로 표현되는 거듭제곱 분포power-law distribution는 x-y의 로그-로그 플롯(log-log plot), 즉 x축을 log(x), y축을 log(y)로 도시했을때 직선 분포 log(y-b) = log(a) - klog(x)를 나타냅니다. 여기서 지수exponent 부분의 k 값은 Power Law의 강도, 즉 꼬리가 얼마나 두꺼운지를 결정합니다.
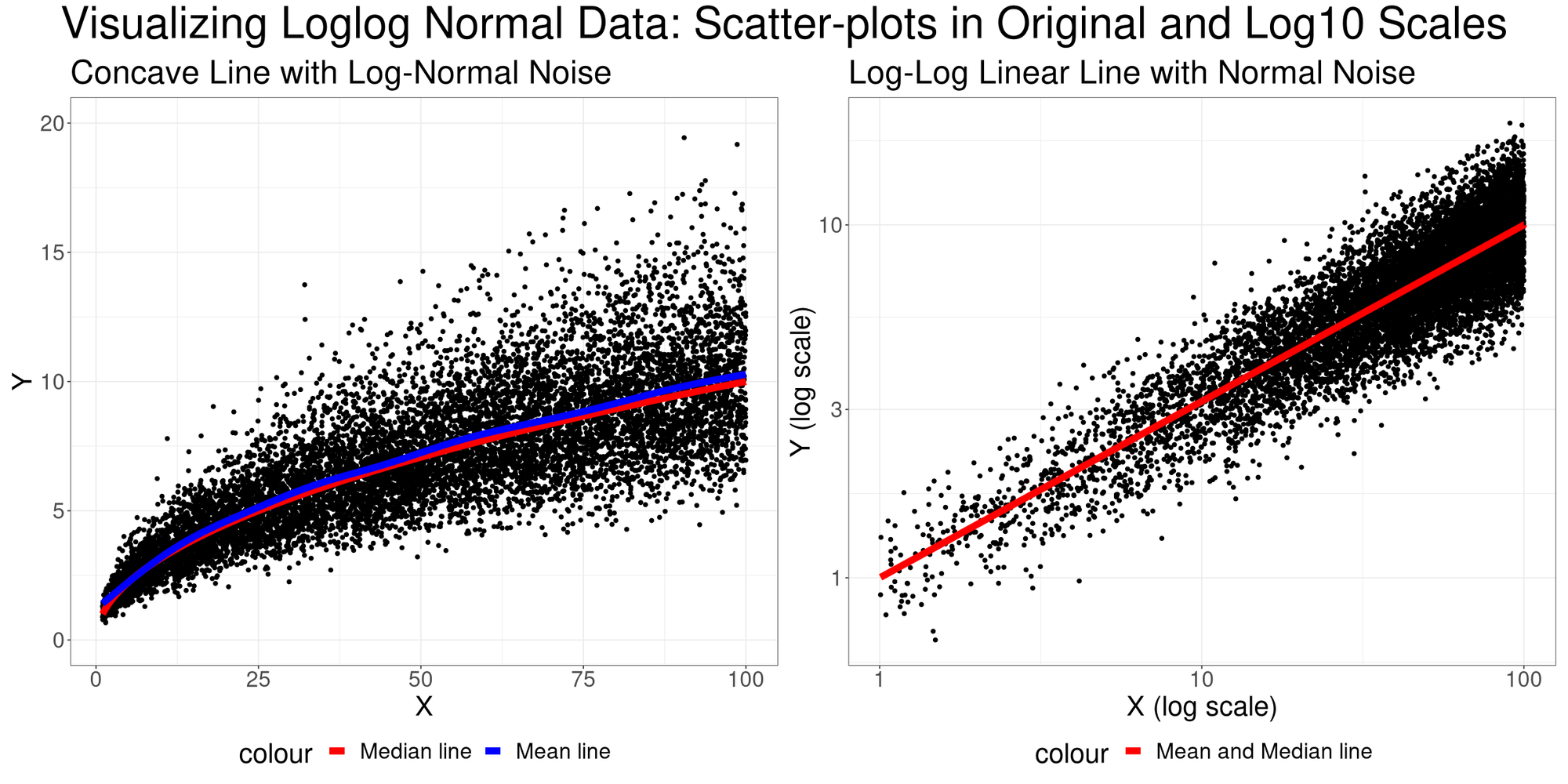
거듭제곱 분포에서 가장 중요한 것은 그 꼬리 부분에 있습니다. 지수함수적으로 급격히 소멸해 거의 의미를 갖지 않는 정규 분포의 꼬리와 달리, 흔히 롱 테일Long tail로 불리우는 Power-law 분포의 꼬리는 결코 무시할 수 있는 크기가 아닙니다. 앞서 예로 들은 성인 남성의 키 분포가 만약 거듭제곱 분포를 따른다면, 지구의 80억 인간 중에는 잠실 롯데타워보다 높은 600m 신장의 사람이 걸어다닐 것입니다.
꼬리가 두꺼운 시스템에서는 실제로 이런 일이 일어납니다. 2억 3백만 개의 웹페이지를 크롤링해 상호간 하이퍼링크 연결을 분석한 한 연구에선 90%의 문서는 10개 이하의 들어오는incoming 링크를 가지는 반면 3개의 페이지는 100만 개 이상의 링크를 받고 있다는 이질적인 분포를 발견하기도 했습니다.

중앙의 평균 정점이 모든 분포를 대표하는 정규분포 시스템과는 달리, 거듭제곱 분포의 시스템에서 핵심 요소는 두꺼운 꼬리에 있습니다. 이 핵심 요소는 전체 네트워크를 강력하게 연결하면서 비정상적으로 많은 링크를 갖고 있는 노드로 우리는 이것을 “허브” 혹은 “커넥터”라 부릅니다. 인간 사회 네트워크에서 커넥터는 서로 다른 인종, 경제 수준, 집단을 잇는 중요한 역할을 합니다. 그들은 경향을 만들고, 중요한 거래를 성사시키며, 유행을 전파하고, 사업을 성공시킵니다.
이러한 커넥터 노드는 정규분포에서처럼 특이한 예외나 소수가 아닙니다. 그들은 인간 관계망, 뉴런 세포, 웹페이지, 함께 작품에 출연한 배우 네트워크-케빈 베이컨 게임- 등 사회학, 생물학, 경제학, 컴퓨터 과학을 넘나드는 온갖 복잡한 시스템에서 발견됩니다. 즉, 커넥터나 허브는 대부분 네트워크의 근본적 속성이며, 정규 분포로 대표되는 무작위적 평등 세계에 대한 강력한 반례입니다.
인간이 종 모양의 정규분포를 보이는 안정적이고 통제 가능한 가변성을 지닌 시스템(평범의 왕국)을 예측 불가능하고 주로 점프를 하면서 움직이는, ‘두꺼운 꼬리’ 시스템으로 변화시킨 것이다. 극단의 왕국에서 흔히 나타나는 ‘두꺼운 꼬리’는 중심에서 멀리 떨어진 사건이 중요한 비중을 차지한다는 의미다. 첫 번째 그래프는 가변성이 있다. 오르내리기는 하지만 가라앉지는 않는다. 반면, 두 번째 그래프는 두드러지게 오르내리지 않다가 갑자기 가라앉아버린다.
…
먼저 극단의 왕국에서는 좋은 일이든 나쁜 일이든 간에 아주 드문 사건이 엄청난 비중을 차지하고 리스크에 노출된 많은 것들을 변화시키지만, 우리가 이를 깨닫지 못하는 경향이 있다. 따라서 이처럼 아주 드문 사건을 활용하거나 예방하는 데 관심을 기울여야 한다. 블랙 스완에 노출되는 것을 두려워하라.
…
이것은 승자독식이라는 극단의 왕국에서 벌어지는 효과를 묘사한다. 그리고 이런 효과는 부의 분배에서 책의 판매에 이르기까지 상당히 일반적으로 나타나는 현상이다.
<안티프래질Antifragile>, 나심 탈레브Nassim Taleb
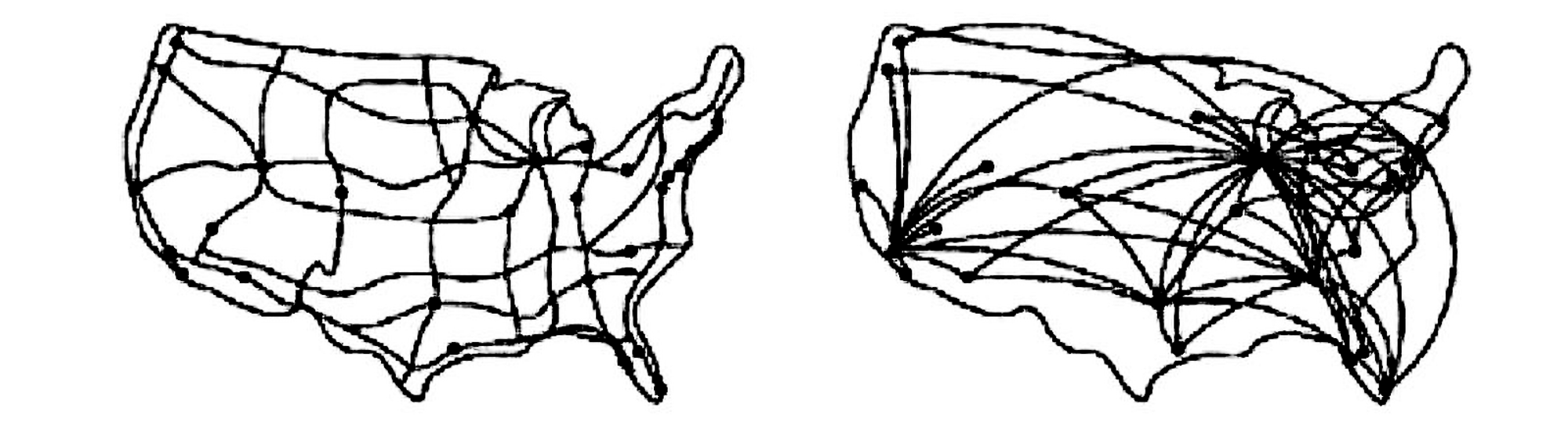
허브와 커넥터의 관점에서, 미국의 고속도로 지도와 항공노선 지도의 차이는 정규분포 시스템과 거듭제곱분포 시스템의 구조적 차이를 시각적으로 잘 보여줍니다. 고속도로 지도에서 도시는 곧 노드이고 고속도로는 각 도시를 연결합니다. 여기서 각 노드는 상대적으로 균일한 연결선link 수 분포를 갖고 있고, 노드당 연결선 수를 도시하면 푸아송 분포와 같은 그래프를 얻습니다.
반면 각 공항이 노드이고 항공편이 각 공항을 연결하는 항공노선 지도에서 각 노드가 갖는 연결선 분포는 위와 대조적입니다. 이례적으로 많은 노드와 연결선을 갖는 소수의 허브와 소수의 링크를 갖는 대다수의 노드가 공존합니다. 허브를 중심으로 불균등unevenness하고 연속적인 위계만이 존재하는 거듭제곱 분포를 보이는 것이 이러한 네트워크의 특징입니다. 이런 분포는 푸아송 분포와 달리 정점highest point이 존재하지 않고, 양쪽으로 끝없이 펼쳐지기에 <링크>의 저자와 그 연구팀은 이를 scale-free 네트워크로 부르기도 합니다.
재밌게도 이 네트워크는 고정된 것이 아니기 때문에 시간에 따라 양극화가 더 심해지는데, 이는 지극히 자연적인 원리로도 볼 수 있습니다. 시간에 따라 거듭제곱 분포를 따르는 시스템이 어떻게 형성될까요? 그리고 이것이 왜 자연적인 과정일까요?
How to model power-law system?
다시 처음의 디너 파티로 돌아와, 사회적 관계 네트워크가 어떻게 형성되는지 살펴보겠습니다. 모델의 규칙은 단순합니다. 100명의 참여자가 고정되어 있고, 시간에 따라 랜덤한 두 사람을 연결하는 관계 링크를 추가합니다. 충분한 시간이 흐르고 나면 이 무작위 네트워크는 몇 개의 클러스터를 갖게 되고, 100개의 링크가 생성될 때쯤이면 거대한 하나의 클러스터가 형성됩니다. 또한 각 사람이 알고 있는 사람의 수의 분포는 정규분포를 따릅니다. 이것이 에르되시-레니 무작위 네트워크Erdos-Reney Random Network로 불리는 네트워크 모델링의 출발점입니다.
<링크>의 저자 A.L. 바라바시는 다양한 현상에서 등장하는 거듭제곱 법칙 분포에서 착안해, 이러한 무작위 네트워크 모델에 의문을 갖기 시작했습니다. 실제로 우리가 아는 디너 파티에서 각 사람이 맺은 관계의 분포는 정규분포를 따르지 않고, 사실은 조금 더 양극화되는 것을 알고 있습니다. 파티가 끝나면 친화력이 좋은 어떤 사람들은 대부분의 사람들과 이야기를 나누고 오지만, 다른 어떤 사람들은 구석에서 두세 사람과만 깊은 관계를 맺고 나오기도 합니다. 실제 사회의 관계망 네트워크는 훨씬 더 양극화된 분포를 갖고 있습니다. 소수의 허브-인싸와 아싸는 명백히 구분됩니다. 심지어는 사회적 관계가 많은 사람에게 더 많은 사회적 관계의 기회가 주어지는 Rich-Get-Richer 양극화 현상이 나타나기도 합니다.
1999년 바라바시는 무작위 모델이 현실을 더 잘 설명하려면 다음의 두 가지 규칙을 추가해야 한다는 아이디어를 바탕으로 비행기 위에서 논문의 초안을 휘갈겨 완성합니다. 이 논문 <Emergence of scaling in random networks>는 사이언스지에 출판되었는데, 2024년 현재 피인용수가 45,000회를 넘길 정도로 많은 호응을 이끌어 냈습니다. 그가 기존의 무작위 시스템에 추가할 것을 제안하는 두 규칙은 다음과 같습니다.
- 시간에 따라 노드의 개수는 증가한다. Networks expand continuously by the addition of new vertices
- 링크를 많이 가지고 있는 노드가 새로운 링크를 부여받을 가능성이 더 높다. And new vertices attach preferentially to already well connected sites

무작위 네트워크에 팽창하는 네트워크와 차별적인 선호도라는 두 조건을 추가하면 일정 시간 t가 지난 후 파티에 있는 각 참여자들이 알고 있는 사람의 수는 거듭제곱 법칙 분포를 따르게 됩니다. 실제로 위 규칙을 따라 직접 시뮬레이션을 해볼 수 있습니다. 여기서 링크의 개수에 따라 차등적인 선호도를 어떻게 정의하는지에 따라 Power Law의 꼬리 두께가 달라지게 됩니다. 저는 양극화를 적정 수준으로 유지시키기 위해 다음과 같이 로그를 취한 log_10(normalized weight: # of links + 2)을 선호도 값으로 사용했습니다.
바라바시 네트워크 시뮬레이션 코드
```python
%%
import numpy as np
from collections import defaultdict
class Person:
def init(self, id) -> None:
self.id: int = id
self._friends: set[int] = set()
@property
def num_friends(self) -> int:
return len(self._friends)
def add_friend(self, person: "Person") -> bool:
if person.id in self._friends:
return False
self._friends.add(person.id)
return True
class Party:
def __init__(self) -> None:
self._total_relationships = 0
self.participants: list[Person] = []
def simulation_step(self) -> None:
self.participants.append(Person(id=len(self.participants)))
if len(self.participants) < 2:
return
while True:
[this, other] = np.random.choice(self.participants, size=2, replace=False, p=self._norm_weights)
if not this.add_friend(other):
continue
other.add_friend(this)
break
self._total_relationships += 1
@property
def _norm_weights(self):
weights = np.array(np.log10([p.num_friends + 2 for p in self.participants]))
return weights / weights.sum() if weights.sum() > 0 else None
def relationship_dist(self) -> list[tuple[int, int]]:
dist = defaultdict(int)
for p in self.participants:
dist[p.num_friends] += 1
return [(k, v) for k, v in dist.items()]
def relationship_dist_log(self):
dist = defaultdict(int)
for p in self.participants:
dist[p.num_friends] += 1
return np.log10(np.array([(k + 1, v + 1) for k, v in dist.items()]))
%%
party = Party()
for t in range(10000):
party.simulation_step()
%%
import seaborn as sns
import matplotlib.pyplot as plt
import matplotlib.ticker as ticker
import pandas as pd
import numpy as np
sns.set_theme(style="whitegrid")
f, (ax1, ax2) = plt.subplots(1, 2, figsize=(13, 6.5))
df = pd.DataFrame(party.relationship_dist(), columns=["num_friends", "num_people"])
sns.scatterplot(data=df, x="num_friends", y="num_people", ax=ax1)
ax1.axhline(0, color='black', linewidth=0.5)
ax1.set_xlabel("# of relationships")
ax1.set_ylabel("frequency")
df = pd.DataFrame(party.relationship_dist_log(), columns=["num_friends", "num_people"])
sns.scatterplot(data=df, x="num_friends", y="num_people", ax=ax2)
sns.regplot(data=df, x="num_friends", y="num_people", ax=ax2)
ax2.axhline(0, color='black', linewidth=0.5)
ax2.set_xlabel("# of relationships (log_10)")
ax2.set_ylabel("frequency (log_10)")
ax2.xaxis.set_major_formatter(ticker.FuncFormatter(lambda x, pos: "{:.0e}".format(np.power(10, x))))
ax2.yaxis.set_major_formatter(ticker.FuncFormatter(lambda x, pos: "{:.0e}".format(np.power(10, x))))
plt.show()
```
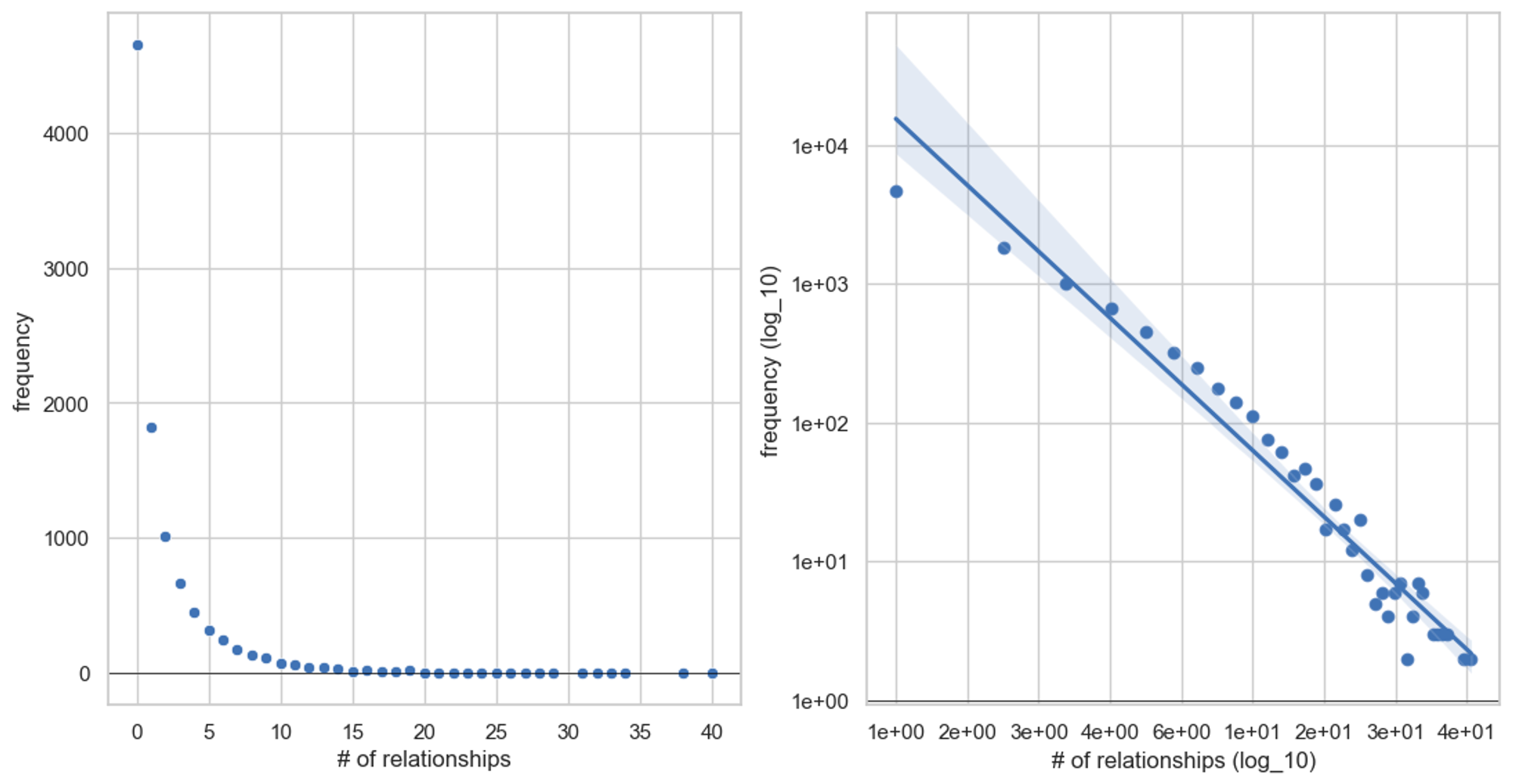
이러한 네트워크 진화이론은 자연이 여러 복잡계를 창조해내는 과정을 재구성함으로써 현실 세계의 구성 메커니즘을 이해하는 출발점을 제공합니다. 또한 복잡하게 연결된 세계에 대한 거듭제곱 법칙에 정당성을 부여하며 우리의 이해의 장을 넓혀 줍니다.
Power Law is Eating the World
세계는 점점 더 복잡하고 거대한 시스템으로 변모하고 있습니다. 복잡계 속에서 Power Law가 지배하는 영역이 넓어지며 불평등이 심화되고 쏠림 현상과 통합·거대화의 물결이 강해지고 있습니다.
그래프 이론은 그 구조에 애매모호함이 전혀 없는 정규적 그래프regular graph에만 거의 전적으로 초점을 맞추어왔다. 하지만 인터넷이나 세포와 같이 복잡한 시스템이 고찰의 대상이 되면서 정규적 그래프는 정상적인 것이라기보다는 오히려 예외적인 것으로 간주되기에 이르렀다.
<링크Linked>, A.L. 바라바시Barabási
지금은 설상가상으로 극단의 왕국이 더욱 넓어지고 있다. 승자 독식 효과는 더욱 두드러지게 나타나서 작가, 기업, 사상, 음악가, 운동선수들은 세계적으로 성공해야 하며, 그렇지 않으면 아무 것도 아니다. 지금은 사회·경제 영역에서 거의 모든 것들이 블랙 스완의 지배를 받기 때문에 예측 가능성을 현저하게 약화시킨다. 우리는 최고가 되기 위해서 끊임없이 세련된 것을 추구하면서, 우리가 이해할 수 없는 영역을 더욱더 넓혀간다.
<안티프래질Antifragile>, 나심 탈레브Nassim Taleb
우리는 복잡계와 초연결의 세계 속에서 Power Law의 존재를 인식하고 그 인과에 주목해야 합니다. 거듭제곱 법칙이 지배하는 시스템에서, 봉우리의 경사가 양쪽으로 나뉘는 분수령은 초기값의 미세한 차이가 전체에 막대한 영향을 미칠 수 있는 나비효과를 불러 일으킵니다. 시초마을에서의 행운과 경로 의존성은 동등한 경쟁자들의 희비를 가르는 눈가린 재판관의 역할을 합니다.
간단히 말하자면 멱법칙power law은 피할 수 없는 것이었다. 체계적이고, 클라이너퍼킨스와는 대조적으로 ‘준비된 마인드’를 갖춘 파트너십조차도 그것을 피할 수는 없었다.
...
마찬가지로 가장 파괴적인 지진은 그보다 규모가 작은 지진들을 모두 합친 것보다 몇 배나 더 강력하며, 대도시들은 모든 작은 도시들을 합친 것보다 인구가 몇 배나 더 많다.
…
그것은 일종의 자연법칙이었다. 사실 그것은 벤처투자자들을 지배하는 법칙이었다. 과거, 현재 그리고 확실히 미래에도 가치 있는 틈새시장을 독점하는 스타트업은 수백만 개의 자신을 차별화하지 않은 경쟁업체보다 더 많은 가치를 지닐 것이다.
…
오히려 이러한 성공은 ‘적절한 때에 적절한 장소에 있는 것’, 즉 행운에서 비롯되었다. 살가닉의 곡 실험에서와 마찬가지로, 행운과 경로 의존성이 벤처캐피털 업계에서 누가 승자가 될 것인가를 설명하는 것으로 보였다.
…
무엇보다도 멱법칙이 갖는 논리를 기억하라. 성공에 따르는 보상은 명예로운 좌절에 따르는 비용보다 훨씬 더 클 것이다.
<The Power Law: Venture Capital and the Making of the New Future>, Sebastian Mallaby
정말로 자기 회사를 차린다면, 그때는 회사의 운영 과정에서 거듭제곱법칙을 반드시 기억해야 한다. 가장 중요한 것들은 오직 하나씩뿐이다. 5장에서 봤던 것처럼 ‘하나의 시장이 다른 모든 시장보다 더 나을 것이다.’ 보통 하나의 유통 전략은 다른 모든 유통 전략을 압도한다. 시간도, 의사결정도 모두 거듭제곱법칙을 따른다. 따라서 어느 한순간은 다른 모든 순간보다 중요하다.
<제로 투 원Zero to One>, 피터 틸Peter Thiel
얼핏 내가 속한 계가 예측 불가능성이 지배하고 카오스 이론을 따르는 것처럼 보일때 우리는 초연한 관찰자의 자세를 견지해야 한다고 믿습니다. 그 기저에 Power Law와 복잡계의 질서가 존재하고 이는 몹시 자연적이라는 믿음이 있다면, 우리는 우리의 무지를 인정하고 호기심 많은 관찰자의 마음으로 자연을 탐구해야 한다고 생각합니다.
Power Law는 지극히 자연적인 법칙이자 무질서에서 질서로의 전이입니다. 상전이에 대한 연구는 이에 대한 통찰을 제공하는데, 제멋대로 돌아다니던 물 분자들은 어떤 임계온도 이하로 냉각되었을 때 마법처럼 일제히 같은 스핀으로 바뀌며 한 방향을 가리킵니다. 이러한 돌연한 전이는 “어떻게 무질서에서 질서가 생겨나는가?”라는 중요한 질문에 대한 열쇠를 제공합니다.
1960년대에 물리학자들에 의해 수집된 실험적 증거들은 금속이 전이 온도에 가까워질 때 몇 가지 핵심적인 수치들이 멱함수 법칙을 따름을 알려주었습니다. 예를 들어, 원자들 간의 신호가 교환되는 거리를 뜻하는 상관 길이correlation length는 클러스터의 결합도를 의미하는데, 임계 온도에 가까워질수록 스핀들이 서로 아는 길이는 넓어지고, 이에 따라 같은 방향을 향하는 스핀의 비율에 의해 결정되는 자력의 크기 역시 멱함수 법칙을 따라 급격히 증가합니다. 이러한 양성 피드백 플라이휠은 어떤 임계점에서 급격한 상태의 전이를 가져옵니다.
1970년대 초에 등장한 윌슨의 재규격화Renormalization 이론은 개별 원자를 분리해 생각하지 않고 원자 전체를 하나의 군으로 커뮤니티화해 다루면서 상전이에 대한 이해를 크게 높였습니다. 그는 환원주의적인 분해의 논리에서 벗어나 전체 군에 적용되는 여러 거듭제곱 법칙을 밝혀냈고, 그 성과로 1982년에 노벨 물리학상을 수상했습니다. 보통 자연의 값과 양은 음성 피드백과 길항작용을 토대로 정규분포를 이룹니다. 하지만 상전이 시스템에서 무질서한 물 분자에서 질서로 가는 길은 자기 조직화self-organization라는 강력한 힘에 의해 유지되며 거듭제곱 법칙에 따라 움직입니다. 이는 단지 거듭제곱 법칙이 특수한 상황에 적용되는 하나의 수식이 아니라, 복잡계에서 자기 조직화를 통해 무질서를 질서로 바꾸고 엔트로피를 낮추는 과정을 일반적으로 설명하는 근본 원리임을 시사합니다.
Power Law에 대한 믿음과 이해를 가지고 있을때, 우리는 그 현상에 당황하거나 분하지 않고 초연한 관찰자의 시선에서 복잡계에 적용되는 질서의 아름다움을 마주할 수 있습니다. 희망컨대 우리는 관찰자의 시선을 견지하여 시스템의 피상과 현상에 대한 반응에 그치지 않고, 구조와 위상에 대한 통찰로 이어지길 기대합니다.
많은 사람들은 기독교의 승리를 오늘날 나사렛의 예수라고 알려진 역사적 인물이 제공한 메시지 덕분이라고 칭송한다. 오늘날의 마케팅 전문가들이라면 그의 메시지가 “점착성이 높다(sticky)” 고 표현할 것이다. 다른 많은 종교적 운동들이 불발탄이 된 데 비해, 그의 메시지는 사방으로 울려 퍼지고 세대에서 세대로 끈질기게 전달될 만큼 끈끈하다는 것이다. 하지만 기독교의 성공의 진정한 공로는 예수를 한번도 만난 적이 없는 한 독실한 정통파 유대교도에게 돌아가는 것이 마땅하다.
…
어떻게 하여 바울의 노력이 성공할 수 있었을까? 그는 기독교가 유대교를 넘어서 널리 전파되기 위해서는 기독교도가 되기 위해 넘어야만 하는 높은 장벽을 허물어버려야 한다는 사실을 잘 이해했다.
...
하지만 바울은 이것만으로는 충분하지 않다는 것을 잘 알고 있었다. 메시지는 전파되어야만 했다. 그는 로마에서 예루살렘에 이르는 서기 1세기의 문명화된 세계에서, 사회적 네트워크에 대한 자신의 경험적 지식을 활용하고자 했다. 그는 12년 동안 10,000마일 가까이 걸었다. 하지만 그가 무작위적으로 돌아다닌 것은 결코 아니다. 그는 당시의 가장 큰 공동체들에 도달하고자 했으며, 신앙이 싹터서 가장 효과적으로 전파될 수 있는 장소와 사람들을 접촉하려고 했다. 그는 신학과 사회적 네트워크를 똑같이 효과적으로 사용할 줄 알았던, 기독교에 있어서 최초의 그리고 가장 뛰어난 세일즈맨이었던 것이다.
…
마피아 보이와 바울 사이에는 커다란 차이점이 있다. 마피아 보이의 행동이 파괴적인 것이었던 반면, 바울은—비록 초기의 의도는 그렇지 않았지만—초기 기독교 공동체들 사이를 잇는 교량의 역할을 하였다. 하지만 둘은 뭔가 중요한 것을 공통적으로 갖고 있다. 둘 다 네트워크의 마스터(master)였던 것이다. 물론 둘 다 네트워크라는 개념을 의식하지 않았을지 모르지만, 그들의 성공의 열쇠는 그들의 행동에 효과적인 매개체를 제공한 복잡한 네트워크의 존재 바로 그것이었다.
…
바울은 첫 번째 세기에 당시의 신앙을 실어 나르고 전파할 수 있는 유일한 네트워크였던 사회적 종교적 링크의 마스터였다. 그렇지만 둘 다 그들의 행동을 도와주었던 힘의 정체를 충분히 인식하지는 못했다.
…
우리는 이제 그 해답이 네트워크를 항해(navigate)할 줄 아는 그들의 능력만큼이나, 네트워크의 구조(structure)와 위상(topology)에 있다는 것을 안다.
<링크Linked>, A.L. 바라바시Barabási